| |
|
|
|
|
|
|
|
|
|
|
|
Last updated
June 2, 2007 |
|
|
|
| |
|
| Polariton Propagation in the Linear Regime |
  
|
|
|
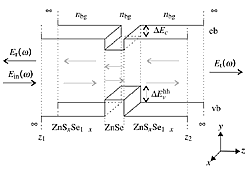
Visualization of the slab geometry for a ZnSe/ZnSSe heterostructure (Schumacher et al., PRB 70, 235340 (2004)).
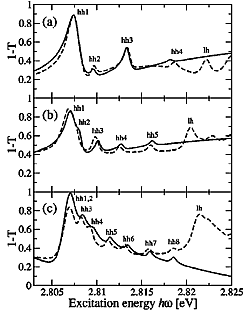
Comparison of theory and experiment for linear transmission spectra for layer thicknesses of 20, 28, and 40nm (Schumacher et al., PRB 70, 235340 (2004)).
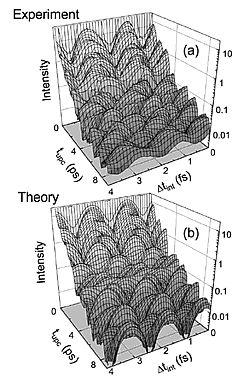
Time-resolved transients of the transmitted intensity through a 25nm ZnSe slab for different delay times between the two phase-locked pulses, showing the coherent control of the polarization in the different polariton modes (Kudyk et al., PRB 73, 235345 (2006)).
|
|
Polaritons and the additional boundary
conditions (ABCs) problem
Since the introduction of the polariton concept the proper description of a propagating light field interacting with the excitonic resonances of a semiconductor medium has been a long standing problem. For the idealized case of propagation inside an infinitely extended semiconductor, the eigenmodes of the propagating light field coupled to the excitonic states can be easily formulated since in this situation the exciton relative and center-of-mass (COM) motion are decoupled.
Complications arise from the inclusion of sample surfaces where an external light field is coupled to the polariton modes and where the polaritons radiatively decay into photons. In the past, macroscopic approaches have been introduced which continue using the excitonic susceptibility of the spatially homogeneous (infinitely extended) medium. In this case the inclusion of sample surfaces requires so-called additional boundary conditions (ABCs). The original proposal of Pekar requires the vanishing of the macroscopic polarization at the semiconductor surface. Other approaches suggest that the spatial derivative or a linear combination of the polarization and its derivative should vanish at the sample surface.
Unfortunately the results for the excitonic transmission and reflection spectra in thin semiconductor layers strongly depend on the particular treatment of boundaries within the macroscopic models. These ambiguities can be avoided within a microscopic formulation of boundary conditions which are imposed on the solution of a two-particle Schrödinger equation for the electron-hole motion under the influence of Coulomb interaction which is directly coupled to Maxwell's equations for the description of the propagating light field.
Another effect that has to be included in macroscopic approaches is the reduced excitonic polarization near surfaces due to finite extension of the exciton relative motion. So-called dead-layers (leading to an effectively reduced sample thickness) have often been used in the past as a fit parameter. We have studied polariton effects in ZnSe/ZnSSe heterostructures as a model material system for shallow confinement within a direct comparison between transmission experiments and calculations using microscopic boundary conditions. For this shallow confinement situation, a breakdown of the dead-layer concept has been demonstrated since the application of Pekar’s ABCs requires an effective sample thickness which even exceeds the thickness of the confinement potential.
In a subsequent study we have demonstrated the coherent control of the polarizations of the heavy-hole exciton-polariton modes and their beatings in time-resolved pulse-transmission experiments using a phase-locked pulse pair. This method was successfully used to switch the polarizations of selected polariton modes and to manipulate the corresponding quantum beat structures in the transients. The results clearly show that decay time of the coherent polarization and, hence, the radiative decay of the ensemble of excited polariton modes can be coherently manipulated.
|
|
|
Involved persons and collaborations:
theory:
Stefan Schumacher, University of Bremen, Germany
Gerd Czycholl, University of Bremen, Germany
Frank Jahnke, University of Bremen, Germany
experiment:
Iryna Kudyk, University of Bremen, Germany
Tobias Voss, University of Bremen, Germany
Ilja Rückmann, University of Bremen, Germany
Jürgen Gutowski, University of Bremen, Germany
Arne Gust, University of Bremen, Germany
Gabriela Alexe, University of Bremen, Germany
Detlef Hommel, University of Bremen, Germany |
|
|
|