Four-wave mixing instabilities

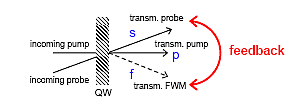
Schematic of a typical pump-probe setup with a single quantum-well. The basic feedback mechanism between probe and (background-free) FWM direction that drives the instabilities is indicated.

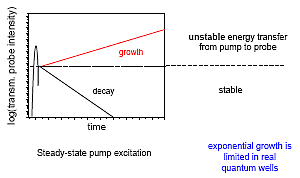
Illustration that shows the two regimes, (i) the usual stable regime where the probe signal exponentially decays over time, and (ii) the unstable regime where under steady-state pump excitation the probe signal exponentially grows over time.

Introduction

In recent years, four-wave mixing (FWM) induced optical instabilities have been the subject of intense theoretical and experimental research in a variety of different physical systems. It has been demonstrated that these instabilities can be exploited, e.g., to utilize extremely efficient optical switches operating at very-low light intensities (down to the few-photon level), for the generation of entangled photons, or - on a more fundamental level - for studying the microscopic mechanisms driving these instabilities.

In semiconductor-based systems excitonic nonlinearities can give rise to optically induced FWM instabilities. However, in contrast to atomic systems, excitation must be limited to those spectral regions where excessive excitation-induced dephasing (EID) can be avoided and where simultaneously excitonic nonlinearities lead to an efficient wave-mixing feedback between probe and background-free FWM direction.

Our theoretical analysis of FWM instabilities in quantum-well based systems (single QWs, and planar microcavities) is based on two different approaches: (i) a fully microscopic many-particle theory which allows the time-domain calculation of the semiconductor polarization dynamics as a response to external light pulses, (ii) a stability analysis of the equations of motion which describes the aforementioned polarization dynamics in the limit of steady-state pump excitation. Both approaches supplement each other and give insight into different aspects of our results.

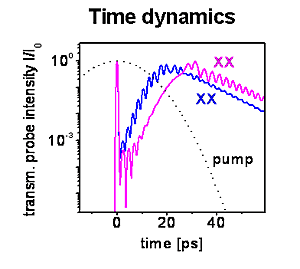
Time-resolved probe pulse transmission that exponentially grows after the initial probe pulse has passed as long as the pump pulse is strong enough to drive the instability. Results are shown for two different pump frequencies (see figure below).

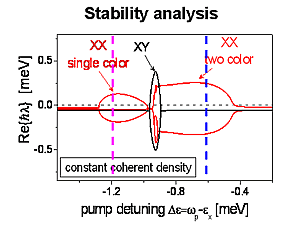
Stability of the probe and FWM modes under steady-state pump excitation. Eigenvalues with a real-part larger than zero give rise to exponentially growing modes over time (unstable modes). Three different regions of instability are found driven by FWM processes involving the excitation of bound biexcitons.

Four-wave mixing instabilities in single quantum wells

Based on a microscopic many-particle theory, we predict large optical gain in the probe and background-free four-wave mixing directions caused by excitonic instabilities in semiconductor quantum wells. For a single quantum well with radiative-decay limited dephasing in a typical pump-probe setup we discuss the microscopic driving mechanisms and polarization and frequency dependence of these instabilities.

In a single semiconductor quantum well (QW) only FWM involving the excitation of bound biexcitons can for pump-excitation spectrally below the exciton resonance and for very small polarization dephasing lead to four-wave mixing instabilities.

From a time-domain solution of the equations of motion for the nonlinear probe, FWM, and pump polarization, we find for certain pump detunings and above a certain pump threshold intensity a large energy transfer from the pump into the probe and FWM directions. For the time-domain results shown about two orders of magnitude of time-integrated gain in the probe direction is found. We find similar outgoing fluences in the background-free FWM directions (not shown).

This result is supported by a linear stability analysis that shows different region of instability for pump excitation below the exciton resonance. These instabilities are driven by FWM processes involving the excitation of bound biexcitons.

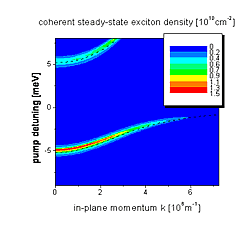
Exciton density for steady-state pump excitation with fixed intensity. Clearly visible are the upper and lower polariton branches in the microcavity system. Excitation-induced dephasing leads to a strongly reduced steady-state density on the upper branch.

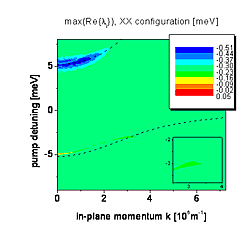
Maximum growth rate (corresponds to decay if negative) in the XX pump-probe polarization configuration. In this polarization configuration no instability is found for the chosen pump intensity.

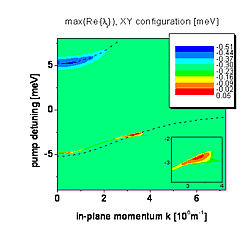
Same figure as the previous one, but for XY pump-probe polarization configuration. Instability is found in a small area around pump excitation under the "magic angle", see also the inset .

Polariton amplification in planar semiconductor microcavities

In the past decade the parametric amplification of polaritons in planar semiconductor microcavities has been the subject of intense experimental and theoretical research. By confining a semiconductor QW inside a planar microcavity very efficient triply-resonant polariton amplification can be achieved because for strong exciton-cavity coupling EID is minimized for excitation on the lower polariton branch.

In a typical pump-probe setup in the co-circular polarization configuration the amplification of a weak probe pulse has been attributed to four-wave mixing processes mediated by the repulsive Coulomb interaction of the exciton constituent of the polaritons excited on the lower polariton branch. Since for a specific pump-polariton in-plane momentum, simultaneous energy and momentum conservation (phase-matching) is best fulfilled for the four-wave mixing processes at work, a pronounced angular dependence of this amplification is observed. Compared to excitonic scattering processes in single quantum wells (without the strong coupling to a confined photon cavity mode), the importance of correlations in the scattering processes of polaritons on the lower polariton branch is strongly reduced. However, even for co-circular pump-probe excitation these correlations are significant for a complete understanding of the experimental results.

In the general framework of four-wave mixing instabilities we investigate the influence of excitonic correlations on the polarization characteristics of the parametric amplification of polaritons in semiconductor microcavities. Whereas for cocircular pump-probe excitation only excitonic scattering in the electron-spin triplet channel (++) plays a role, for excitation with not strictly circularly polarized light pulses excitonic scattering in the electron-spin singlet channel (+-) is expected to contribute to the amplification mechanism, too.

We use a stability analysis of the cavity polariton dynamics to discuss that depending on the pump-probe polarization configuration (co-linear or cross-linear, respectively) excitonic correlations can diminish or enhance the parametric scattering processes. For arbitrary probe polarization and for a microcavity with otherwise perfect in-plane isotropy this many-particle-interaction induced polarization dependence (brought about by the coupling of the two spin subsystems excited with + and - circularly polarized light) can lead to a significant rotation/change of the outgoing (amplified) probe signal's polarization relative to the polarization of the incoming probe.

Excitonic correlations can not only lead to additional dephasing in the system in terms of excitation-induced dephasing which eventually raises the required threshold intensities/densities and therefore weakens the polariton amplification. We have demonstrated that depending on the pump-probe polarization configuration (co-linear or cross-linear, respectively) excitonic correlations additionally -- and in the strong coupling regime more importantly -- can either diminish or enhance the phase-conjugate coupling which is the fundamental driving force for the polariton amplification to occur.

Involved persons and collaborations:

Stefan Schumacher, University of Arizona, Tucson, Arizona, USA
Nai H. Kwong , University of Arizona, Tucson, Arizona, USA
Rolf Binder, University of Arizona, Tucson, Arizona, USA

Arthur L. Smirl, University of Iowa, Iowa City, USA

Funding:

ONR, DARPA, JSOP,
DFG (project No. SCHU 1980/3-1)